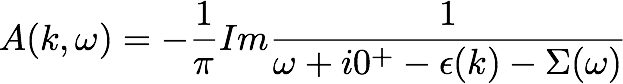Spectral properties of polarons from DMFT
S. Ciuchi
Introduction
In this page I present results obtained by DMFT
for the spectral function of a single particle interacting with non
dispersed phonon (frequency w0). The model I chose is the Holstein model
in which the particle interacts trough a simple local charge
displacement interaction with e-ph coupling constant g. The
interaction parameter lambda is defined as lambda=g^2/w0D where D the
half-bandwidth of the free charge.
Results are shown for the
spectral function which is defined as the imaginary part of the
retarded single particle Green function
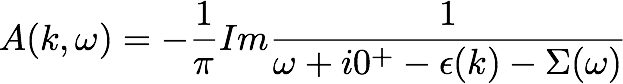
notice that within single site DMFT the self-energy depends only on w not on k.
For illustrative purposes I chose a simple cosine-like dispersion epsilon(k) while the band used to get the self-energy is semicircular.
I also choose to report energies in the hole representation.
Data
are reported for the range of parameters around the polaron crossover
in the adiabatic regime w0/D=0.1. For example in our system for
lambda=0.7 we are approaching the polaron crossover but still in the
non polaronic region. The polaron crossover as seen in A(k,w) is
reported here. What I want to show is the a characteristic feature of the system near
the polaron crossover, i.e. not necessarily within a polaronic regime
but close to it, is the appearance of characteristic multiphonon
resonances at low energy. This multiphonon resonances which are
characteristic of the anti-adiabatic regime (w0>>D) are indeed
present also in the adiabatic regime shown in the figures. Of course
many effects contribute to destroy this typical behaviour. Some of them
are listed below, some others are reported in subsequent studies
of A(k,w) which includes e.g. k dispersion of e-ph g, disorder,
interaction with more than one single phonon have been done
subsequently. Some of them are reported in the non-exaustive bibliography .
The antiadiabatic regime w0>D could be of interest in the case of organic single crystals. An illustrative example of band narrowing with temperature is here.
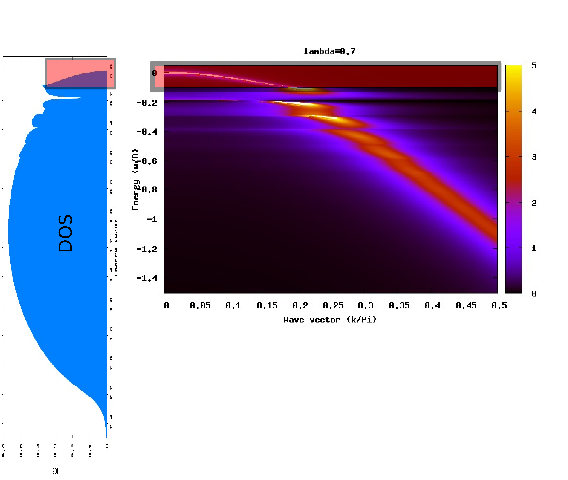
Energy regions in A(k,w) (adiabatic regime)
Approaching
the polaron crossover region at intermediate e-ph coupling in the
adiabatic regime (lambda=0.7 w0/D=0.1 in the following figure) the
spectral function A(k,w) shows three energy scales:
1) Low energy
Coherent (k-dispersed) low energy quasi-particle peak shows on an energy window (w0=phonon frequency) from the Fermi energy
2) Intermediate energy
Above
the coherent energy scale multiphonon resonances appears near the
polaron crossover. They become more evident once the e-ph coupling
increases entering in the polaronic region. At strong coupling resonances extends roughly up to
the edge of the free-electron band, here at intermediate coupling they are visible for a larger energy window.
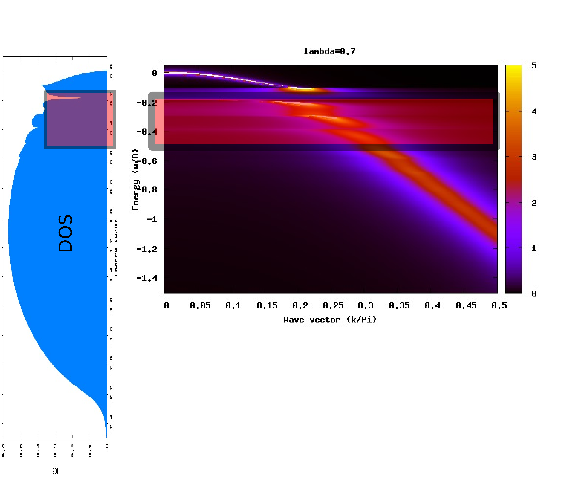
3) High energy
At higher energies a shadow traces the free electron bandwidth. It is a purely incoherent structure.
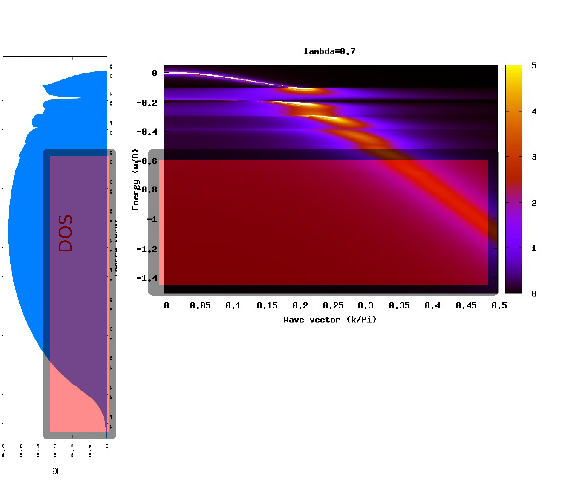
Polaron crossover in A(k,w)
As
the e-ph increases the inchoerent feature which starts at w0 from the
Fermi energy acquires some modulations which develops in almost
undispersed multiphonon resonances for larger couplings. This behaviour
is reminiscent of the polaron crossover seen in others quantities such
as the ground-state energy, the kinetic energy etc.
an animation showing the A(k,w) versus lambda
Effects of temperature in A(k,w) (adiabatic regime)
At
intermediate e-ph coupling, in the proximity of polaron crossover, increasing the temperature from T<<w0 to T=w0 will produce
phonon resonances due to the absorption of phonons by the thermal bath
at energies higher that the Fermi energy. At the same time the coherent peak becomes broader and extends up to higher energies.
an animation showing the A(k,w) versus temperature
Band narrowing with temperature in A(k,w) (antiadiabatic regime)
At weak/intermediate e-ph coupling, even well below the polaron
crossover, increasing the temperature from T<<w0 to T=w0 will narrow
the polaronic band when w0>2D. Here I chose w0=2D and lambda=0.5.
Also a weak signature of the first phononic resonance is seen at low
energy.
an animation showing the A(k,w) versus temperature in the anti-adiabatic regime
Effects of disorder in A(k,w)
Here
is shown the effect of a weak gaussianly distributed diagonal disorder
at intermediate e-ph coupling (see this work reported in the bibliography). Notice that the disorder is more
effective to destroy the multiphonon resonances than to destroy
the coherence of the quasiparticle peak.
an animation showing the A(k,w) versus disorder